जिल्हा परिषद माध्यमिक विद्यालय, विडूळ ता . उमरखेड जि. यवतमाळ
Online Exam
Class - 10th, Sub - Mathematics- I , Marks - 40, Time - 2 Hours
Date - 06 / 04 / 2021 , Timing - 12 : 00 ते 2 : 15
-----------------------------------------------------------------
Q. 1 (A) For every subquestion 4 alternative answers are given. Choose the correct answer and write the alphabet of it: 04
i. Find the value of Dx for the equation 4𝑥 + 3 𝑦 = 19 and 4 𝑥 − 3 𝑦 = −11.
A) 24 B) 0
C) −24 D) 108
ii. What is the value of discriminant for the quadratic equation x² – 2x - 3
= 0 ? A) -16 B) 16 C) 8 D) 4
iii. First four terms of an A.P., are……………………whose first term is -2 and
common difference is -2. (A) -2,0,2,4 (B) -2,4,-8,16 (C) -2,-4,-6,-8 (D) -2,-4,-8,-16
iv. When three coins are thrown the number of sample points in the sample space
are ........ A) 6 B) 12
C) 36 D) 8
Q.1. B. Solve the following subquestions: 04
i. The cost of the book is 5 rupees more than twice the cost of a pen. Show
this using linear equation by taking Cost of book(x) and cost of a pen(y).
ii. Write the given quadratic equation in standard form. m (m – 6) = 9
Q 2 A)
iii. Write the formula of the sum of first n terms for an A.P.
iv. Write a sample space if two coins are tossed simultaneously.
Q.2. A. Complete and write any two activities from the following: 04
ii) Complete the following activity to find the value of discriminant for
4x² – 5x + 3 = 0.
Activity:
4x² – 5x + 3 = 0
a= 4 , b = …… , c = 3
b² - 4ac = (-5)² – (….) x 4 x 3
= (….) – 48
b²
- 4ac = ……
iii)Common difference, d = ?
for the given
A.P., 7,14,21,28.........
Activity :-
Here t1=7, t2=14, t3=21, t4= ......
t2 - t1= ......
t3 – t2= 7
t4 – t3= ......
Therefore,
common difference d= .......
Q.2. B. Solve any four subquestions from the following: 08
i. If (2, −5) is the solution of the equation 2𝑥 − 𝑘 𝑦 = 14 then find k
=?
ii. If roots of a quadratic equation 3y2+ ky+ 12= 0 are real and equal then
find the value of ‘k’.
iii. 1,6,11,16......Find the 18th term of this A.P.
iv. If two coins are tossed, find the probability of event getting no head on both
the coins.
v. Using variables 𝑎 𝑎𝑛𝑑 𝑏 write any two equations whose solution is
(0,2)
प्र. 3 A. खालीलपैकी कोणतीही एक कृती सोडवा. 03
i. The sum of the two-digit number and the number obtained by interchanging the digits is 132. The digit in the ten’s place is 2 more than the digit in the unit’s place.
Complete the activity to find the original number.
Activity: Let the digit in the unit’s place is y and the digit in the ten’s place is 𝑥.
∴ The number = 10 𝑥 + 𝑦
∴ The number obtained by interchanging the digits = .....
∴ The sum of the number and the number obtained by interchanging the digits = 132
∴ 10 𝑥 + 𝑦 + 10 𝑦 + 𝑥 = ......
∴ x + y = ........ (I) ,
By second condition, Digit in the ten’s
place = digit in the unit’s place + 2
∴ x - y = 2 . . . (II)
equation (I) and (II)
∴ x = ........ y = ......
Ans: The original number = .....
ii. Find the sum of natural numbers between 1 to 140, which are divisible by 4.
Activity :- Natural numbers between 1 to 140 divisible by 4 are, 4,8,12,16,......136
Here d=4, therefore this sequence is an
A.P. a=4, d=4, tn=136, Sn= ?
tn = a+ (n-1)d
...... = 4+ (n-1)x4
....... = (n-1)x4
n= ......
Now
Sn = n / 2 + ( a + tn )
Sn=17 X ......
Sn = .........
Therefore, the sum of natural numbers between 1 to 140, which are
divisible by 4 is .......
प्र. 3. B . पुढील कोणतेही दोन उपप्रश्न सोडवा. 06
i. The length of the rectangle is 5 more than twice its breadth. The perimeter of a rectangle is 52 cm then find the length of the rectangle.
ii. Form a quadratic equation if the roots of the quadratic equation are 2 + √7 and 2 - √7 .
iii. If tn=2n-5 is the nth term of an A.P., then find its first five terms.
iv. If two dice are rolled simultaneously, find the probability of the following events.
i) Event A : The sum of the digits on the upper faces is at least 10.
ii) Event B : The sum of the digits on the upper faces is 33.
Q.4. Attempt any two subquestions from the following: 08
i. A train covered a certain distance at a uniform speed. If the train would
have been 6 km/h faster, it would have taken 4 hours less than the
scheduled time. And ,if the train was slower by 6 km/h it would have taken 6
hours more than the scheduled time. Find the length of the journey.
ii. If the roots of the given quadratic equation are real and equal then find the value of ‘m’.
(m-12) x² + 2 (m-12) x + 2 = 0
iii. Shubhankar invested in a national savings certificate scheme. In the
first year he invested Rs.500, in the second year Rs.700, in the third
year Rs.900 and so on. Find the total amount that he invested in 12
years.
Q.5. Attempt any one subquestion from the following: 03
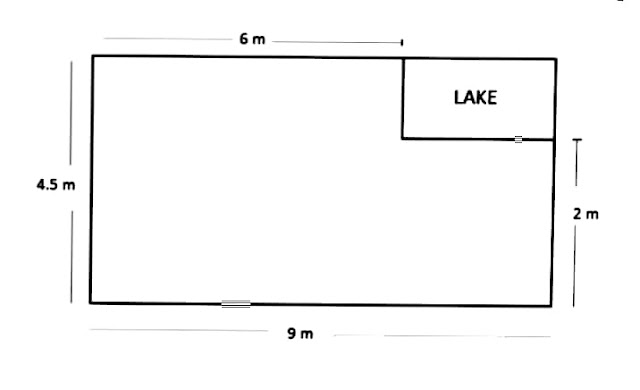
i. A missing helicopter is reported to have crashed somewhere in the rectangular region shown in the figure .
What is the probability that it crashed inside the lake shown in the figure ?
ii. Form a quadratic equation such that one of its roots is 5. Form a quadratic equation for it and write.
( For the formation of word
problem you can use quantities like age, rupees or natural numbers.)
(sample solution for the above example is given below students can
take another number to form another example)